PrograZine #6 - Optimisation stochastique: le recuit simulé

[ edito | sommaire | contribution | contacts ]

[>Optimisation stochastique: le recuit simulé<]

Jean Debord
JDebord@compuserve.com

>Introduction

Les méthodes de descente aléatoire pure

Le recuit simulé

>Les méthodes de descente aléatoire pure

             Choisir X0 initial ; évaluer F(X0) ; itération r := 0 
             (1) A l'itération r+1, générer un vecteur aléatoire X à partir de Xr 
             si F(X) < F(Xr) alors Xr+1 := X 
             si critère d'arrêt non vérifié alors faire r := r + 1 et aller en (1) 
             si critère d'arrêt vérifié alors arrêter ; (Xr, F(Xr)) est la solution approchée.

>Le recuit simulé

>Principe

  p = exp(-(E2 - E1) / kT)            (1)

Une diminution de la fonction sera toujours acceptée.

Une augmentation de la fonction sera acceptée avec une probabilité définie selon une formule analogue à (1), avec ici k = 1 et T un paramètre formel jouant le rôle de la température.

>Implémentation

             Choisir X initial 
             Calculer T0 
             tant que critère d'arrêt non vérifié faire : 
                  m := 0 ; 
                  répéter jusqu'à ce que m = NT (nombre d'itérations à la température T) 
                       Générer un vecteur aléatoire Y voisin de X 
                       dF = F(Y) - F(X) 
                       Appel fonction Accepte(dF, T) 
                       si Accepte est vrai alors X := Y 
                       m := m + 1 
                  fin répéter 
                  Diminuer la température 
             fin tant que

             si dF < 0 alors 
                  Accepte := vrai 
             sinon 
                  A := exp(- dF / T) 
                  si Random(0, 1) < A alors Accepte := vrai sinon Accepte := faux 
             fin si

1.Une procédure de détermination de la température initiale :
Au début des itérations, alors qu'on est éloigné du minimum, on choisit une probabilité d'acceptation élevée, p.ex. p = 0,5. On peut alors effectuer un certain nombre de tirages aléatoires et calculer la valeur médiane M des augmentations de la fonction (la médiane est la valeur qui partage une distribution en deux parties égales). La température initiale T0 s'en déduit par :
p = exp(- M / T0) = 0,5 d'où: T0 = - M / ln p ~ 1,44 M
l

2.Un schéma de décroissance de la température (le "recuit") :
On choisit habituellement une décroissance géométrique :
Tn+1 = RT Tn soit : Tn= T0 (RT)n (2)
l

3.Un critère d'arrêt :
On peut arrêter les itérations lorsque la température est devenue inférieure à une fraction donnée de la température initiale, p. ex. Tn < 10-6 T0
Il ne s'agit là que de l'algorithme de base. De nombreuses améliorations sont possibles (voir p.ex. le programme ASA de Lester Ingber).

>Programmation en Turbo Pascal

>L'unité OPTIM.PAS

la méthode de Marquardt (voir cours sur la régression non linéaire).

la méthode BFGS (Broyden-Fletcher-Goldfarb-Shanno).

la méthode du simplexe.

>Types et variables globales

       type
         TFuncNVar = function(X : PVector) : Float;

Pour la signification du type PVector, voir le cours sur le calcul matriciel.

       const
         SA_Nt        : Integer = 50;   { Nb d'itérations à chaque température }
         SA_Cv        : Float   = 0.5;  { Coef. de variation des nombres aléatoires }
         SA_MinSigma  : Float   = 1.0;  { Ecart-type minimal des nombres aléatoires }
         SA_SigmaFact : Float   = 0.1;  { Facteur de réduction global de l'écart-type }
         SA_NCycles   : Integer = 1;    { Nombre de cycles de recuit }

1.Le tirage d'un nouveau vecteur aléatoire à partir du vecteur courant X se fait selon une loi normale centrée sur X et telle que l'écart-type du paramètre xi est donné par :

MinSigma + Cv * |xi|

où MinSigma et Cv sont initialisés à SA_MinSigma et SA_Cv, respectivement, et diminués à chaque changement de température, de sorte que leurs valeurs finales soient à SA_SigmaFact de leurs valeurs initiales. Cette diminution progressive de l'écart-type permet de réduire la taille de la portion d'espace explorée à mesure que l'on se rapproche du minimum.

2.En modifiant la valeur de SA_NCycles, on peut effectuer plusieurs cycles de recuit simulé, en recalculant à chaque fois la température initiale. Ceci permet de relancer l'algorithme s'il s'est arrêté à trop grande distance du minimum.

       const
         WriteLogFile : Boolean = False;       { Indique si le fichier doit être écrit ou non }
         LogFileName  : String  = 'OPTIM.LOG'; { Nom du fichier }

La température

La dernière valeur acceptée de la fonction

Le nombre d'augmentations de la fonction

Le nombre d'augmentations acceptées

>Procédure de recuit simulé

  function SimAnn(Func           : TFuncNVar;
                  X              : PVector;
                  Lbound, Ubound : Integer;
                  MaxIter        : Integer;
                  T_Ratio        : Float;
                  var F_min      : Float) : Integer;

  En entrée
  ------------------------------------------------------------
  Func    = Fonction à minimiser
  X       = Coordonnées approchées du minimum
  Lbound  = Indice de la première variable
  Ubound  = Indice de la dernière variable
  MaxIter = Nombre d'étapes de recuit
  T_Ratio = Rapport de la température finale à la température initiale

  En sortie
  ------------------------------------------------------------
  X       = Coordonnées affinées du minimum
  F_min   = Valeur de la fonction en X

1.Le générateur de nombres aléatoires est réinitialisé à chaque appel de la fonction. On obtiendra donc des résultats différents à chaque appel. Il est conseillé de lancer plusieurs fois la fonction et de comparer les résultats.

2.Le facteur de réduction de la température RT est déterminé par les valeurs de MaxIter et T_Ratio selon l'équation (2) :

RT = (T_Ratio)1/MaxIter

p. ex. avec MaxIter = 100 et T_Ratio = 10-6 on a :

RT = (10-6)1/100 ~ 0,87

3.La fonction retourne toujours 0.

>Programme de démonstration

F(x, y) = x^2 + y^2 - cos(12x) - cos(18y)

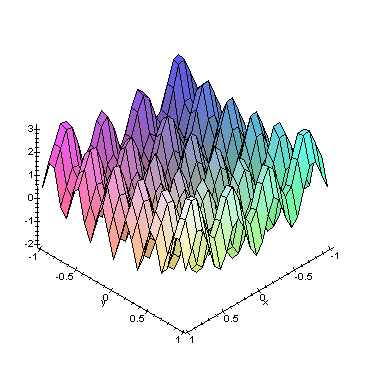
Figure 1 Graphe de la fonction F(x, y) = x2 + y2 - cos(12x) - cos(18y) (Graphique réalisé avec Maple->LIEN)

    x    |  0,0153   |   -0,0025   |    -0,0010  |  -0,0063  |  -0,0022
    y    | -0,0055   |    0,0004   |    -0,0014  |  -0,0033  |  -0,0013
---------|-----------|-------------|-------------|-----------|-----------
    F    |  -1,98    |    -2,00    |     -2,00   |   -2,00   |   -2,00

      |  Marquardt     |    BFGS    |   Simplexe
      |----------------|------------|--------------
x     |    2,06        |   -1,03    |     1,03
y     |   -3,12        |   -1,39    |     0,00
F     |   12,13        |    1,02    |    -0,92

>Conclusion

Ce document est la propriété de Jean Debord. La rédaction ainsi que l'auteur déclinent toutes résponsabilité vis-a-vis des conséquences que pourrait entrainer le contenu de cet article.